NCERT Solutions for Class 10 Maths Chapter 12:- Students क्लास 10th की गणित के अध्याय 12 में आपको वृत्तों के छायांकित भाग और त्रिज्य खंड के क्षेत्रफल के बारे में बताया गया है। आप इस अध्याय में जानेंगे की किसी भी वृत्त में यदि कुछ भाग को निकाल दिया जाए या छायांकित कर दिया जाय तो उस क्षेत्र का क्षेत्रफल और संगत चाप की लम्बाई कैसे निकाली जाती है।

Summary (सारांश) of Areas Related to Circles
- त्रिज्या r वाले वृत्त की परिधि = 2 π r
- त्रिज्या r वाले वृत्त का क्षेत्रफल = π r2
- त्रिज्या r वाले वृत्त के त्रिज्यखंड, जिसका कोण अंशों में θ है, के संगत चाप की लम्बाई होती है यह है फार्मूला
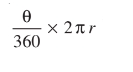
- त्रिज्या r वाले वृत्त के एक त्रिज्य खंड , जिसका कोण अंशों में θ है , का क्षेत्रफल होता है यह है फार्मूला
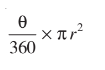
- एक वृत्तखंड का क्षेत्रफल = संगत त्रिज्य खंड का क्षेत्रफल – संगत त्रिभुज का क्षेत्रफल
वृतों से संबंधित क्षेत्रफल के उदाहरण


स्टूडेंट्स यदि आप चैप्टर 12 से संबंधित अन्य उदहारण (Examples) देखना चाहते हैं तो आप आर्टिकल में नीचे दी गयी पीडीऍफ़ फाइल में उदाहरण देख सकते हैं।
प्रश्नावली 12.1 (वृत्त का परिमाप और क्षेत्रफल) के सॉलूशन्स


प्रश्नावली 12.2 (त्रिज्यखंड और वृत्तखंड का क्षेत्रफल) के सॉलूशन्स

प्रश्नावली 12.3 (समतल आकृतियों के संयोजनों के क्षेत्रफल) के सॉलूशन्स
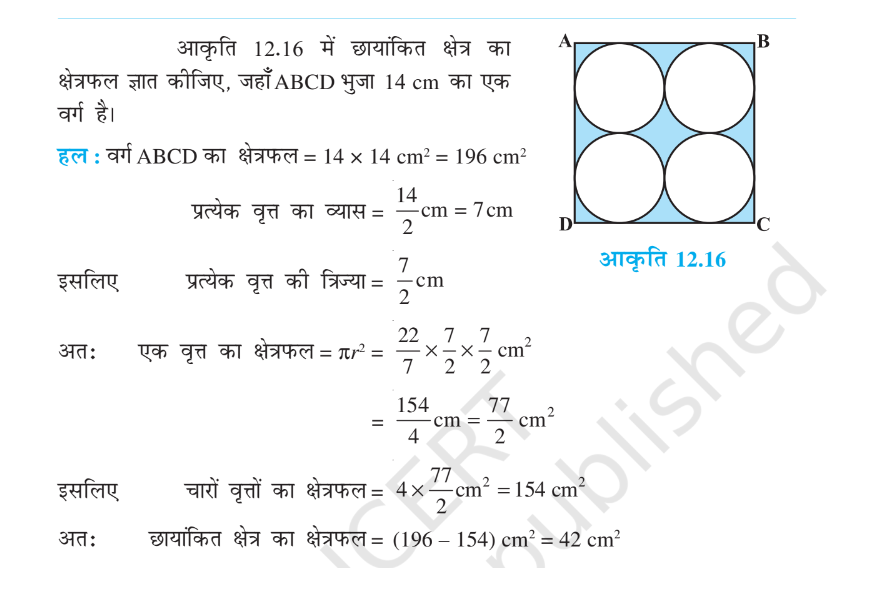
स्टूडेंट्स यदि चैप्टर 12 के अन्य प्रश्नों के solutions देखना चाहते हैं तो आप हमारे द्वारा आर्टिकल में दी गयी पीडीऍफ़ फाइल में Solutions देख सकते हैं।
किसी भी वृत्त के चारों ओर के परिमाप की लम्बाई को वृत्त की परिधि कहा जाता है। वृत्त की परिधि का सूत्र 2 π r होता है। जहाँ r वृत्त की त्रिज्या है और π का मान 22 / 7 है।
किसी भी वृत्त में त्रिज्य खंड वह भाग होता है जो वृत्त की दो त्रिज्याओं और चाप से घेरकर बनता है।
वृत्त खंड और त्रिज्य खंड के क्षेत्रफल में निम्नलिखित संबंध है
एक वृत्तखंड का क्षेत्रफल = संगत त्रिज्य खंड का क्षेत्रफल – संगत त्रिभुज का क्षेत्रफल









